Googleがコミュニティモビリティレポートを公開している。これはGoogleアカウントのロケーション履歴を有効にしているユーザー(サンプルベース)のデータに基づいた移動データで、2020 年 1 ⽉ 3 ⽇〜2 ⽉ 6 ⽇の 5 週間における該当曜⽇の中央値を基準とした増減のデータになっている。詳細はモビリティ レポートの CSV ドキュメントを参照。今回はこのデータを使って、Pythonで時系列クラスタリングをすると同様にPythonのtslearnを使って時系列クラスタリングを行う。
環境
モビリティレポートの可視化
モビリティレポートのcsvには世界中のデータが含まれるが、ここでは日本の都道府県ごとのデータのみを使う。まずはcsvをPandasのDataFrameとして読み込んで中身を確認。sub_region_1が都道府県のカラムで、retail_and_recreation_percent_change_from_baselineからresidential_percent_change_from_baselineが場所カテゴリごとの移動データになっている。
import pandas as pd # Googleモビリティレポートのファイルパス # 2020年1月3日から2月6日の5週間の曜日別中央値を基準とした値 MOBILITY_CSV_GOOGLE = 'Global_Mobility_Report.csv' dfg = pd.read_csv(MOBILITY_CSV_GOOGLE) dfg.info()
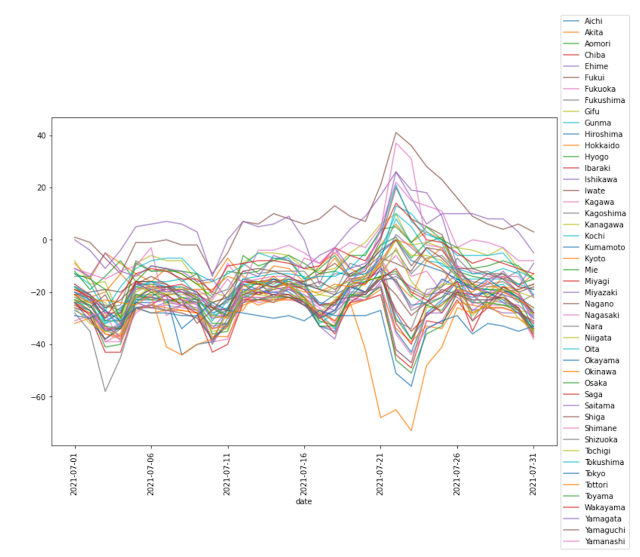
7月の都道府県ごとのtransit_stations_percent_change_from_baseline(公共交通機関の拠点)のデータを可視化してみる。
%matplotlib inline import matplotlib.pyplot as plt import pandas as pd # Googleモビリティレポートのファイルパス # 2020年1月3日から2月6日の5週間の曜日別中央値を基準とした値 MOBILITY_CSV_GOOGLE = 'Global_Mobility_Report.csv' # 対象とする場所のカテゴリ # 公共交通機関の拠点(例: 地下鉄、バス、電車の駅)など MOBILITY_CATEGORY = 'transit_stations_percent_change_from_baseline' dfg = pd.read_csv(MOBILITY_CSV_GOOGLE) # 都道府県ごとのデータを取得 dfg_jp = dfg[dfg['country_region_code']=='JP'].dropna(subset=['sub_region_1']) # 都道府県のチェック pref = dfg_jp['sub_region_1'].unique() print(pref) assert len(pref) == 47 # 日付をインデックス、都道府県をカラムとするDataFrameに変換 dfg_cat = dfg_jp.set_index(['date', 'sub_region_1'])[MOBILITY_CATEGORY].unstack() # 2021年7月のデータを取得 dfg_cat_jul = dfg_cat['2021-07-01':'2021-07-31'] # データのプロット ax = dfg_cat_jul.plot(figsize=(12,8), alpha=0.75, rot=90); ax.legend(loc='center left', bbox_to_anchor=(1.0, 0.5)) plt.show()
クラスター数を決める
データをk-means法で時系列クラスタリングするが、k-means法では事前にクラスター数を決める必要がある。クラスタリングの前にシルエット値からクラスター数を決定する。シルエット値はk-means法の最適なクラスター数を選択するでも使用しているが、今回はSelecting the number of clusters with silhouette analysis on KMeans clusteringを参考にシルエット値をプロットして確認してみる。なお、メトリックとしてユークリッド距離を使う。
以下はクラスター数2~5の範囲でシルエット値を算出してプロットするコード。scikit-learnにはデータごとのシルエット値を返してくれるsilhouette_samplesメソッドがあるがtslearnにはないので自作した。平均シルエット値が1に近く、プロット幅がなるべく均等になるクラスター数がよいと言われている。
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import pandas as pd
from tslearn.clustering import TimeSeriesKMeans, silhouette_score
from tslearn.preprocessing import TimeSeriesScalerMinMax
from tslearn.utils import to_time_series_dataset
from scipy.spatial.distance import cdist
from sklearn.metrics import silhouette_samples as sklearn_silhouette_samples
# Googleモビリティレポートのファイルパス
# 2020年1月3日から2月6日の5週間の曜日別中央値を基準とした値
MOBILITY_CSV_GOOGLE = 'Global_Mobility_Report210814.csv'
# 対象とする場所のカテゴリ
# 公共交通機関の拠点(例: 地下鉄、バス、電車の駅)など
MOBILITY_CATEGORY = 'transit_stations_percent_change_from_baseline'
def silhouette_samples(X, labels, **kwds):
"""シルエット値の計算
ユークリッド距離の計算方法は以下tslernのコードを参照
https://github.com/tslearn-team/tslearn/blob/42a56cc/tslearn/clustering/utils.py#L66-L197
"""
X_ = X.reshape((X.shape[0], -1))
sklearn_X = cdist(X_, X_, metric='euclidean')
# 計算済みのデータを渡すのでmetric='precomputed'にする
return sklearn_silhouette_samples(X=sklearn_X,
labels=labels,
metric='precomputed',
**kwds)
def plot_silhouette_scores(ts_data, silhouette_values, n_clusters, km):
"""シルエット値のプロット
以下のコードをほぼコピー
https://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html#sphx-glr-auto-examples-cluster-plot-kmeans-silhouette-analysis-py
"""
cluster_labels = km.labels_
centers = km.cluster_centers_
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(ts_data) + (n_clusters + 1) * 10])
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhouette score of all the values
ax1.axvline(x=np.mean(silhouette_values), color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(ts_data[:, 0], ts_data[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors, edgecolor='k')
# Labeling the clusters
# centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
s=50, edgecolor='k')
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()
def show_silhouette_scores(ts_data, dates):
# クラスター数2-5を確認
for n_clusters in range(2, 6):
print('クラスター数 =', n_clusters)
km = TimeSeriesKMeans(n_clusters=n_clusters, metric='euclidean', verbose=False, random_state=1).fit(ts_data)
assert len(km.labels_) == 47
print('クラスタリング結果 =', km.labels_)
silhouette_values = silhouette_samples(ts_data, km.labels_)
silhouette_avg = np.mean(silhouette_values)
print('シルエット値平均 =', silhouette_avg)
plot_silhouette_scores(ts_data, silhouette_values, n_clusters, km)
dfg = pd.read_csv(MOBILITY_CSV_GOOGLE)
# 都道府県ごとのデータを取得
dfg_jp = dfg[dfg['country_region_code']=='JP'].dropna(subset=['sub_region_1'])
# 都道府県のチェック
pref = dfg_jp['sub_region_1'].unique()
print(pref)
assert len(pref) == 47
# 日付をインデックス、都道府県をカラムとするDataFrameに変換
dfg_cat = dfg_jp.set_index(['date', 'sub_region_1'])[MOBILITY_CATEGORY].unstack()
# 2021年7月のデータを取得
dfg_cat_jul = dfg_cat['2021-07-01':'2021-07-31']
# データのプロット
ax = dfg_cat_jul.plot(figsize=(12,8), alpha=0.75, rot=90);
ax.legend(loc='center left', bbox_to_anchor=(1.0, 0.5))
plt.show()
# 正規化
ts_data = TimeSeriesScalerMinMax().fit_transform(dfg_cat_jul.values.transpose())
prefs = dfg_cat_jul.columns
dates = dfg_cat_jul.index
show_silhouette_scores(ts_data, dates)
実際にはクラスター数2から5の結果が表示されるが、以下はクラスター数4の結果。平均シルエット値だけをみると他のクラスター数がよさそうだが、ここではクラスター数4を採用する。
時系列クラスタリングの結果を可視化
クラスター数が決まったので、時系列クラスタリングして、クラスターごとの平均を可視化してみる。
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import pandas as pd
from tslearn.clustering import TimeSeriesKMeans, silhouette_score
from tslearn.preprocessing import TimeSeriesScalerMinMax
from tslearn.utils import to_time_series_dataset
from scipy.spatial.distance import cdist
from sklearn.metrics import silhouette_samples as sklearn_silhouette_samples
# Googleモビリティレポートのファイルパス
# 2020年1月3日から2月6日の5週間の曜日別中央値を基準とした値
MOBILITY_CSV_GOOGLE = 'Global_Mobility_Report210814.csv'
# 対象とする場所のカテゴリ
# 公共交通機関の拠点(例: 地下鉄、バス、電車の駅)など
MOBILITY_CATEGORY = 'transit_stations_percent_change_from_baseline'
## シルエット値プロット用の関数は省略 ##
def tsclustering(ts_data, prefs, n_clusters):
km = TimeSeriesKMeans(n_clusters=n_clusters, metric='euclidean', verbose=False, random_state=1).fit(ts_data)
# クラスタリングの結果
result = pd.DataFrame({'clust': km.labels_}, index=prefs)
for clust, g in result.groupby(by='clust'):
print('Cluster: ', clust)
print(g.index)
# クラスターごとの中心をプロット
for i, c in enumerate(km.cluster_centers_):
plt.plot(c.T[0], label=i)
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.show()
dfg = pd.read_csv(MOBILITY_CSV_GOOGLE)
# 都道府県ごとのデータを取得
dfg_jp = dfg[dfg['country_region_code']=='JP'].dropna(subset=['sub_region_1'])
# 都道府県のチェック
pref = dfg_jp['sub_region_1'].unique()
print(pref)
assert len(pref) == 47
# 日付をインデックス、都道府県をカラムとするDataFrameに変換
dfg_cat = dfg_jp.set_index(['date', 'sub_region_1'])[MOBILITY_CATEGORY].unstack()
# 2021年7月のデータを取得
dfg_cat_jul = dfg_cat['2021-07-01':'2021-07-31']
# データのプロット
ax = dfg_cat_jul.plot(figsize=(12,8), alpha=0.75, rot=90);
ax.legend(loc='center left', bbox_to_anchor=(1.0, 0.5))
plt.show()
# 正規化
ts_data = TimeSeriesScalerMinMax().fit_transform(dfg_cat_jul.values.transpose())
prefs = dfg_cat_jul.columns
dates = dfg_cat_jul.index
# show_silhouette_scores(ts_data, dates)
n_clusters = 4
tsclustering(ts_data, prefs, n_clusters=n_clusters)
時系列クラスタリングの結果は以下の通り。4連休での差が大きい。4連休で最も移動が減少しているクラスター2には東京、大阪、愛知などの大都市圏が含まれる。逆に4連休に移動が上昇したクラスター1,3には地方の都道府県が含まれている。クラスター2に沖縄県が入っているが、これは台風で天候が悪かった影響と考えられる。



0 件のコメント:
コメントを投稿